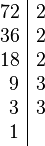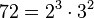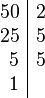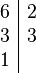2014-01-11

MKT

Oraingoan gai berria dugu: MKT (MULTIPLO KOMUN TXIENA) ateratzea. 
Ikusi orri hauek:

Zenbaki batzuen multiplo komun txikiena aurkitzeko, lehenik, zenbakietako bakoitza zenbaki lehenetan deskonposatu behar da. Hurrena, deskonposizioko zenbaki lehenak elkarrekin biderkatu behar dira, eta haietako bakoitza zenbakietako edozeinetan agertzen den gehienezko aldi-kopurua adina aldiz hartuta. Kontzeptu hau polinomioekin ere defini daiteke.
Adibidez, 72 eta 50 zenbakien m.k.t.:
\begin{array}{r|l} 72 & 2 \\ 36 & 2 \\ 18 & 2 \\ 9 & 3 \\ 3 & 3 \\ 1 & \end{array}
72 = 2^3 \cdot 3^2 \,
\begin{array}{r|l} 50 & 2 \\ 25 & 5 \\ 5 & 5 \\ 1 & \end{array}
50 = 2 \cdot 5^2 \,
m.k.t.(72, 50) = 2^3 \cdot 3^2 \cdot 5^2 = 1800

Zatikien  batuketa

Multiplo komun txikiena izendatzaile desberdineko frakzioak batzeko erabil daiteke, frakzioen izendatzaileen m.k.t. kalkulatuz, eta frakzio baliokideak bihurtuz batu ahal izateko. Ikus dezagu adibide hau:
\frac {1}{6} + \frac {4}{33}
Batuketa egin ahal izateko, lehenik izendatzaileen (6 eta 33) multiplo komun txikiena kalkulatu behar dugu
\begin{array}{r|l} 6 & 2 \\ 3 & 3 \\ 1 & \end{array}
6 = 2 \cdot 3 \,
\begin{array}{r|l} 33 & 3 \\ 11 & 11 \\ 1 & \end{array}
33 = 3 \cdot 11 \,
hortaz:
\operatorname{m.k.t.} (6,33)= 2 \cdot 3 \cdot 11 = 66
eta orain izendatzailea 66 duten frakzio baliokideak bilatu behar ditugu, batuketa egin ahal izateko::
\cfrac {1}{6} + \frac {4}{33} = \quad \cfrac {1}{6} \cdot \cfrac {11}{11} + \cfrac {4}{33} \cdot \cfrac {2}{2} = \quad \cfrac {11}{66} + \frac {8}{66} = \quad \cfrac {19}{66}